[HDG method] Error illegal dnumsin Assemble BilinearForm 'biform_from_py'

I'm trying to implement a HDG method for the Stokes problem.
[tex]a_h(u_h, v_h) + b_h(v_h, p_h)-b_h(u_h, q_h)+ c_h(p_h, q_h)=\int_\Omega f\cdot v_hdx[/tex]

where
[tex]b_h(v,q) = -\int_\Omega q\nabla\cdot v dx + \sum\limits_{K\in \mathcal{T}}\int_{\partial K}(v-\bar{v})\cdot n\bar{q}ds,[/tex]
[tex]c_h(q, r):=\sum\limits_{K\in \mathcal{T}}\int_{\partial K}h_K(q-\bar{q})(r-\bar{r})ds.[/tex]
Please see the attached ipynb files for more details.
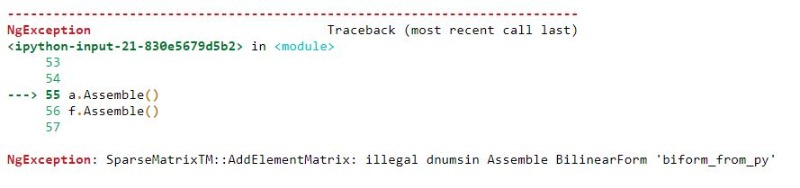
The error is
parseMatrixTM::AddElementMatrix: illegal dnumsin Assemble BilinearForm 'biform_from_py'

when I used When I changed the code to ,
then the error is UmfpackInverse: Numeric factorization failed.

Could you please tell me why this is and how to fixed it?
Thank you so much.

1) You want to use "element_boundary" here. "skeleton" does not give you what you want.
"skeleton" terms are integrals over facets, but there are multiple volume elements attached to a facet.
The term is not well defined. Which of the volume elements attached to a facet should provide "p" and "q"?
With "element_boundary", it is well defined. Every facet is integrated over twice - once as part of the boundary of each volume element.
"skeleton" is usually used when you have jumps between volume elements, something like Here, it does not matter which of the volume elements of a facet provides "p" and which one "p.Other()".
To make this clear, your term, using "skeleton", would be something like this: For "skeleton" to work, though, you have to set "dgjumps=True" in the FESpace: Forgetting this, and using "skeleton" integrals leads to the illegal dnums error you encountered.

2) See the replies to this post from last week as for why your problem is not well posed if we use Dirichlet conditions everywhere and how to fix this issue.

3) There is a typo: should be You can do and look at the matrix entries as a first sanity check. In this case, ALL entries are 0, which leads us to suspect something is off with trial/test functions.

4) Your formulation is wrong should, I think, be You should multiply the divergence criterium by -1, or define p as -p such that you get a symmetric matrix. This is not strictly speaking necessary, but good practice.
The term (v-vbar)*n*pbar is, I believe, wrong. I think it should be a b*n*pbar

Best,
Lukas

Thank you very much for the detailed explanation. This helps me a lot.

Best wishes,
Dong