New Features

Netgen parallelization

Since the third user meeting in July we spent some of our time on optimization and parallelization of the meshing code in Netgen. This post presents the improvements implemented so far.

As can be seen in the diagram below, most of the computation time was spent in mesh optimization. Therefore we started parallelizing the optimization steps one by one. To avoid race conditions and ensure deterministic behaviour (i.e. the same mesh is generated sequentially and in parallel), we used different techniques: For the mesh smoothing ("MeshImprove") we calculate a graph coloring and process one color (i.e. sets of non-adjacent vertices) at a time in parallel. For the other optimizations (e.g. SwapImprove, CombineImprove) we search for possible improvements in parallel. After that, these "candidate operations" are applied sequentially in specific order.

In addition we could improve the search tree for determination of the local mesh size. Instead of a binary search tree we store multiple entries (approx. 100) in the leaves of the tree and thus combine linear search with binary search. Among other small improvements, this reduced the time spent in tree searches, the dominant part in 3D mesh generation, by a factor of 3.

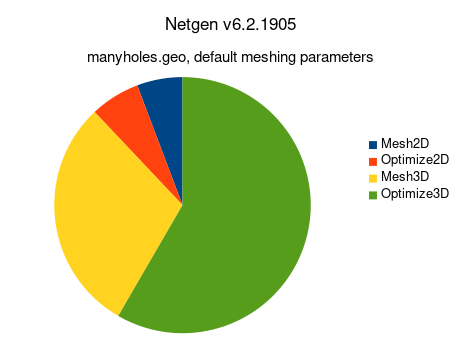
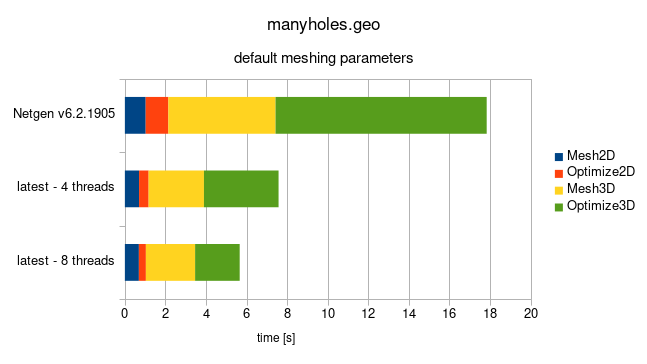
The achieved speed-up is quite consistent across different geometries (CSG, STL, STEP), below are the times for the 'manyholes.geo' tutorial file with default meshing parameters. The optimizations are now running in parallel with according speed-ups. In total, you can expect faster mesh generation by a factor of 2.4-3.2 on a processor with 4 or more cores.

So how can you take advantage of it? There are two new meshing options available in the GUI: "Parallel meshing" enables multithreading in general during mesh generation, and "Number of meshing threads", which controls the number of threads used for mesh generation. By default, the Netgen-GUI uses 4 threads for mesh generation. In python scripts, you can start the TaskManager manually:

import pyngcore as ngcore
ngcore.SetNumThreads(4)
with ngcore.TaskManager():
    geo.GenerateMesh()

In this short article, we show how the new coupling type "HIDDEN_DOF" in NGSolve can be used to make certain methods more efficient. This concerns methods, where (element-local) auxiliary variables are used to define certain types of projections, e.g. L2-Projections / liftings / interpolations. Exemplarily, the procedure will be explained with the help of a Hybrid Discontinuous Galerkin (HDG) method for the Poisson problem where stability is ensured by means of a (Bassi-Rebay-type) $L^2$-lifting technique. 

We can now define generic (quasi-) periodic finite element spaces which work for all the main function spaces (H1, HCurl, HDiv) by creating a finite element space wrapper with a mapping of the degrees of freedom. This wrapper is created from python by calling the generator function Periodic.

Assume you have some mathematical function (such as cylindrical Bessel functions) from some C/C++ library (like the special function package from boost), and you want to use it within CoefficientFunctions. Now you can import it via a small, separate Python module.

We can now specify an integration-rule for the SymbolicBFI, it works like this: